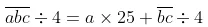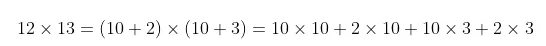范冰冰 女同 若是父母在一运行陪孩子学习数学时就刷到这篇著述,该有多好啊!
发布日期:2024-12-31 01:19 点击次数:194


数主宰着天地。
——毕达哥拉斯
来源 | 《写给孩子的数学之好意思》
作家 | 昍爸、昍妈
01
与男儿的八次对话
对话一
我想和男儿沿路数一数有些许个积木,我刚启齿“1、2、3……”,男儿就打断了我:“爸爸,我们不错两个两个数:2、4、6……这么不是更快吗?我还会 5 个 5 个数:5、10、15……”
对话二
我曾对男儿许下诺言,若是她背满 100 首古诗,我就带她去环球影城玩。某天,在她背完一首古诗后,我问她:“还剩些许首诗,我们就不错去环球影城了?”没猜测她反问我:“昨天还剩几首来着?”我说,23 首。她“狡诈”地答:“那还有 22 首了。”
对话三
我让她算 20 以内的减法,我先问:“14 减 5 等于几?”她回话:“9。”我问她是奈何算的。她说:“14 先减 4,然后再减 1。”我接着问:“15 减 6 等于几?”她很快回话 9。我又问她是奈何算的,她说:“15 比 14 多 1,6 比 5 多 1,是以谜底如故 9。”
对话四
晚饭后,我常常带男儿去买面包和牛奶。有一次,我们买了 8 盒大白兔牌牛奶,我问她:“2 盒牛奶 5 元钱,8 盒些许钱?”她回话:“20 元,因为 2 盒 5 元,是以 4 盒 10 元,8 盒即是 20 元。”
对话五
我领导她尝试进行两位数的减法,先问她 14 减 6 等于几,她答 8。我又问她 24 减 6 等于几,她答 18。我再接着问 34 减 6 等于几,她答 28。我不时问 44 减 6 等于几,她答 38。再问 44 减 16 等于几,她答 28。终末,我问 44 减 26 等于几,她答 18。
对话六
我拿了 9 块巧克力,让男儿分给我、昍妈、昍(她哥哥)和她四个东谈主,她给每东谈主分了 2 块后,说:“爸爸,还有一块不错切成 4 份,给每东谈主分 1 份。”
对话七
我跟她玩比大小的游戏。每个东谈主拿两张牌,然后看谁的牌面上的数字之和大。有一次,她拿了 8 和 17,我拿了 12 和 23,她很寂寞地说:“爸爸,我毋庸加就知谈你的牌比我的牌大了,因为我的 8 比你的 12 小,我的 17 比你的 23 小。”另一次,她拿了 9 和 34,我拿了 11 和 25,这一次,她快乐起来:“爸爸,我毋庸加就知谈我的牌比你的牌大,因为你的 11 只比我的 9 大 2,而我的 34 比你的 25 可大不少呢。”
对话八
我们如故玩比大小的游戏,但此次章程谁的两张牌的牌面数字之差小,谁就赢。有一次,她拿了 16 和 25 这两张牌,而我拿了 12 和 35。这时她就快乐起来:“爸爸,我不减也知谈是我赢了,因为我的 16 比你的 12 大,而我的 25 比你的 35 小,是以我的两张牌靠得更近!”
其实,我从这八次对话判定,年仅五岁的她渐渐找到了“数感”这件宝贝,为什么呢?且听我冉冉谈来。
02
什么是数感?
顾名念念义,数感即是一个东谈主对数的嗅觉——这常常与直观关联。学术界浩繁合计,数感是一个东谈主贯通、关联、勾通和使用数的智商,包括:
知谈数的相对值,能够比拟两个数的大小;
知谈怎样使用数作念出正确判断;
在加、减、乘、除时,知谈怎样天真地使用数;
知谈如安在计数、测量或估算时,制定有用的计谋。
东谈主在早年发展起来的好坏数感是学好数学的重要,因为它将数数与数目接洽起来,能自如和完善对“多”和“少”的贯通,匡助大家猜测数目和测量值,并为更高阶的学习奠定基础。相背,若是清寒精深的数感,那数学平常学不好。数感在数学学习中所演出的脚色就好比在英语学习中,当然拼读里的音素分解在阅读中演出的脚色。
比如,一个孩子在学习盘算 6 加 5 时,若是弗成成功从 6 运行往后数 5 个数,而老是需要从 1、2、3、4、5、6 运行数起,然后再数 7、8、9、10、11,那阐明这个孩子莫得很强的“数感”。
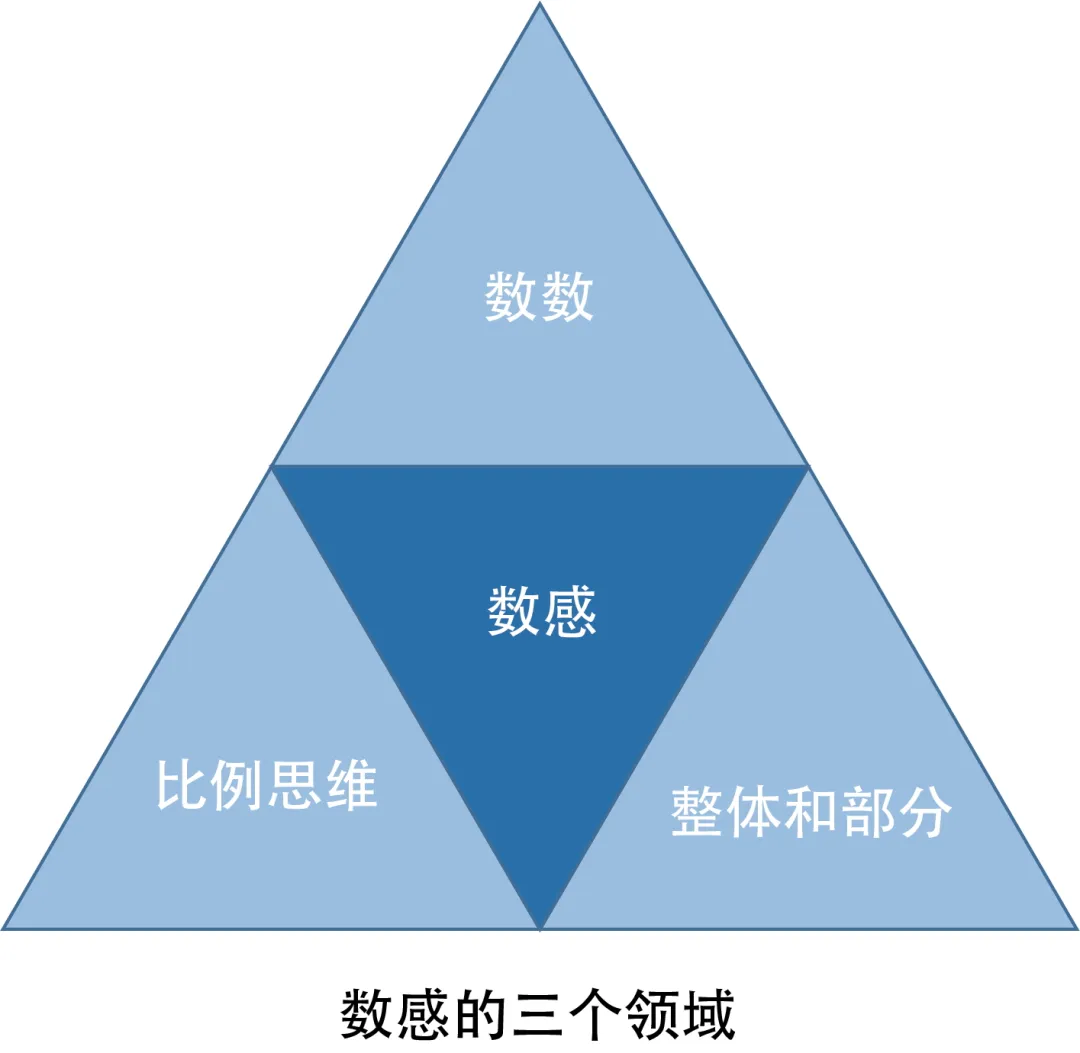
“数感”平常包含三个规模(图 9.1)。
图 9.1
李蓉蓉 麻豆03
数数
数数是将称号与数目接洽起来的智商,它匡助我们贯通数字系统是如缘何 10 个为一组,即以 10 为基数,组织起来的。大巨额数学学习坚苦的东谈主清寒计数手段。对他们来说,贯通和利用数字限定、跨越计数和模式(如奇数和偶数)会显得很坚苦。
数数的形态包括一个一个地数、两个两个数、5 个 5 个数、10 个 10 个数等。在这个经由中,大家不错贯通数的相对限定、奇数和偶数、5 的倍数、10 的倍数等与十进制密切关联的见解。
除了上头的数法,我们还不错增多一些难度,进行底下的考研。
(1) 从 2 运行,以 10 为单元数到 102,再倒数回 2。
(2) 从 1 运行,3 个 3 个数,数到大于 100 截止,再倒数回 1。
(3) 从 3 运行,4 个 4 个数,数到大于 100 截止。
04
比例念念维
数学中的比例念念维用于念念考一个数是另一个数的些许倍,或是几分之一。举例,6 是 3 的些许倍?12 内部有几个 4?中国东谈主口是法国东谈主口的些许倍?
大家不错借助底下的游戏行为和问题考研比例念念维。
(1) 用一根绳索测量你的身高,按身高剪断绳索并用它来找出在教室里或家里,还有什么东西和你的身高一样长。
(2) 在一堆积木中寻找是某个积木块 2 倍大的积木块,或寻找是某个积木一半大小的积木块。
(3) 若是你有 12 块比萨,要分给 4 位一又友,每位一又友应该得到些许块比萨?
(4) 3 根铅笔卖 5 元,那 12 根铅笔卖些许钱?
我在起首提到的对话四中的盘算大白兔牌牛奶的价钱的问题,就需要用最朴素的比例念念维进行念念考。
05
全体和部分
着手设施略数的一部分是什么。比如,8 是由 7 和 1、6 和 2、5 和 3 以及 4 和 4 构成的。再如,7+3=10,其中部分是 7 和 3,而全体是 10。更进一步,23 是由 2 个十和 3 个一构成的。
其实,刚运行战斗分数的时刻,我们即是把分数当作一个全体里的相称的部分来贯通的。我们也不错通过分数来贯通全体和部分的接洽,比如
,1 即是全体。
全体等于部分之和,亦然欧几里得的名著《几何蓝本》里的公理之一。是以,全体和部分不仅体目前数,也体现于形。
本章起首提到的对话三和对话六中的例子,就展现了初步的部分和全体不雅。现实上,小学阶段最重要也最难掌抓的一个运算律——乘法分拨律,亦然源自数的全体和部分之间的接洽。
数感从那儿来?
我们的数感是从那儿来的呢?
直观产生的“数字感”在我们很小的时刻就有了。年仅两岁的儿童就不错自信地识别一个、两个或三个物体,然后,我们材干真确贯通数数的真谛。瑞士脸色学家皮亚杰将这种即刻识别一小群物体数目的智商称为“直感”(subitising)。跟着心智智商的发展,平常在四岁操纵,我们就不错毋庸数数,就能识别出不超过四个一组的物体数目。
东谈主们合计,即使对于大巨额成年东谈主来说,通过“直感”数清的最大数目也即是 5 个。这种手段似乎是基于大脑造成雄厚的模式脸色图像,并将它们与数字接洽起来的一种智商。因此,若是将物体以特定的神志成列,或进行特定的老成和顾忌,东谈主们就有可能识别 5 个以上的物体。一个简便的例子是,若是把 6 个点 3 个一瞥排成两排,就像骰子或扑克牌上的六点图案一样,那东谈主们就不错立即识别出“6 个”。
平常,当目下呈现超过 5 个对象时,东谈主们就必须使用其他的脸色计谋。举例,我们可能将一组 6 个对象视为两组 3 个对象——每组 3 个会立即被认出,然后很快(确凿无分解地)被组合成 6 个。在这种计谋中,不触及现实的对象计数,而是使用“部分 - 部分 - 全体”接洽和快速的脸色加法。也即是说,我们运用了一个数(在这种情况下为数“六”)不错由更小的部分(数“三”)构成,以及“三加三等于六”的学问。这类数学念念维在我们运行上学时就仍是渐渐造成了,我们应该悠闲培养这种念念维,因为它为贯通运算和制定有价值的默系数谋奠定了基础。
哪些游戏行为不错促进早期数感的造成呢?
早期的数字行为最佳使用可转移的物体,举例筹码、积木和小玩物。大巨额东谈主需要具体的告诫,将一组物体在物理上分红多个子组,并将小组组合成更大的组。在这“分分合合”的经由中,我们将对数数、比例念念维、全体和部分有更为成功的体验。有了这些基本色验之后,更多的静态材料,如“点卡”,会变得相称有用。
点卡即是一侧贴着若干单色点的简便卡片。卡片的假想要素是点的数目和点的成列神志。这些要素的多样组合决定了每张卡片的数学结构,从而决定了它们所激励的数的接洽和我们将承袭哪种脸色计谋。
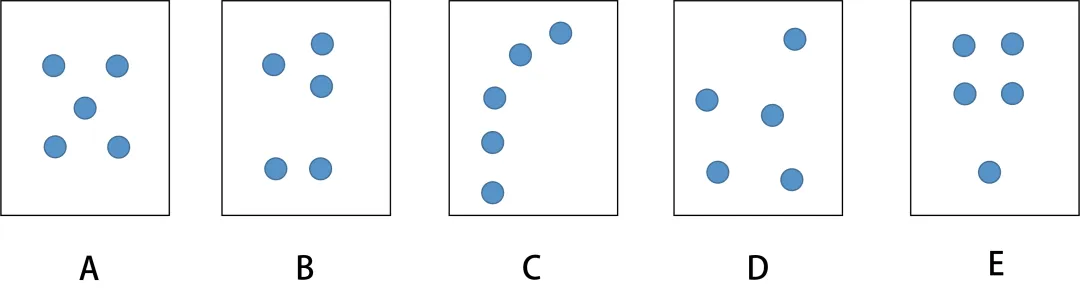
如图 9.2,磋议卡片中的点的成列。每张卡片可能会激励什么样的脸色计谋?字据难度级别,你会将它们按什么限定成列?
图 9.2
卡片 A 是经典的对称成列,因此,我们平常无须使用其他脸色计谋即可立即识别。这可能是最容易措置的 5 个物体的成列神志。
卡片 B 呈现出了了的 2 和 3 的子组,每个子组齐不错立即识别出来。通过老成,确凿通盘东谈主齐能立即回忆起“二加三等于五”的盘算接洽。
卡片 C 的线性成列是最有可能教导计数的成列。然则,许多东谈主会在脸色上将这些点分红“两个和三个”,正如上一张卡片中一样的两组。我们也不错使用其他计谋,比如看到 2 个点,然后数 3、4、5。
卡片 D 不错称为立时成列,尽管现实上这些点是经过悉心组织的,以促进分组的脸色行为。子组的造成神志有好多种,莫得任何特定地点的教导,是以这张卡片不错被视为本系列中最难的一张。
卡片 E 展示了一种饱读吹使用“四加一等于五”的子构成列接洽。
游戏对于加强和发展儿童的早期数感相称有用。在玩中学,我们会好奇艳羡满满。上头提到的卡片是比拟传统的一种点卡,目前市面上比这更好玩的数学游戏有好多,大家不错我方找出来玩。
我们一朝对最多为 10 的数造成了基本的数感,就需要发展好坏的“十感”当作位值和默算的基础。底下的十帧矩形框不错灵验起到这一作用。
十帧是 2×5 的矩形框,其中遗弃了筹码来涌现小于或等于 10 的数,因此,这个游戏对在 10 的领域内发展数感相称有用。筹码的多样成列神志教导我们要对计数这些点承袭不同的脸色计谋,并展现了 10 以内的数与 10 的接洽。
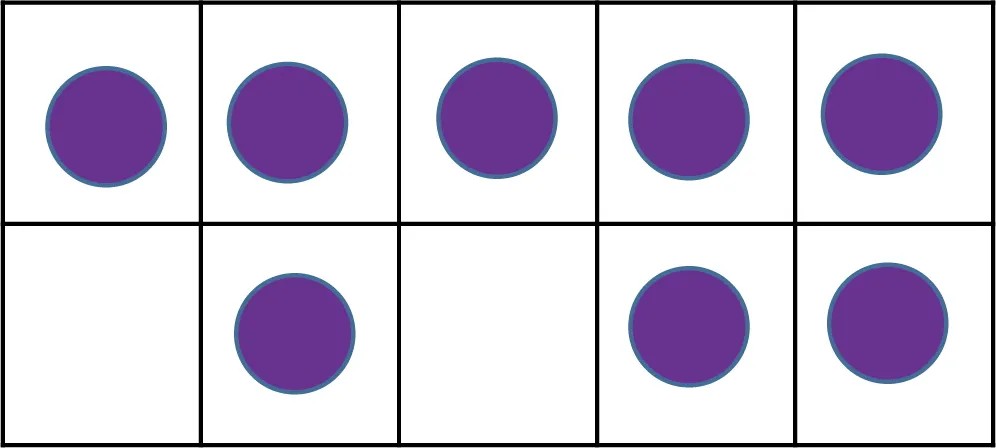
如图 9.3,不雅察底下的三个十帧,图中分解了哪些数?筹码的很是成列使你念念考的数是什么?对于每个数与 10 的接洽,你能说出什么?图 9.3
框 A:有 5 个筹码;通过巡逻帧两头的簇,或者巡逻顶部和底部行中的数,也许不错将其视为“三个和两个”的子组。
框 B:相似有 5 个筹码;不错视为“顶行三个、底部三个”,或“四加一”,或“二加二加一”。值得注重的是,框架里还剩下 5 个空盒子,其全体形态与满盒子的全体形态相似,这促使我们分解到“五加五等于十”。
框 C:这种安排有劲地阐明了“五加五等于十”的念念想。它还涌现了,10 的一半是 5 的主张。若是在莫得提前阐明这是“十帧”的情况下,即使呈现了 5 个筹码,这种主张也不会即刻产生。
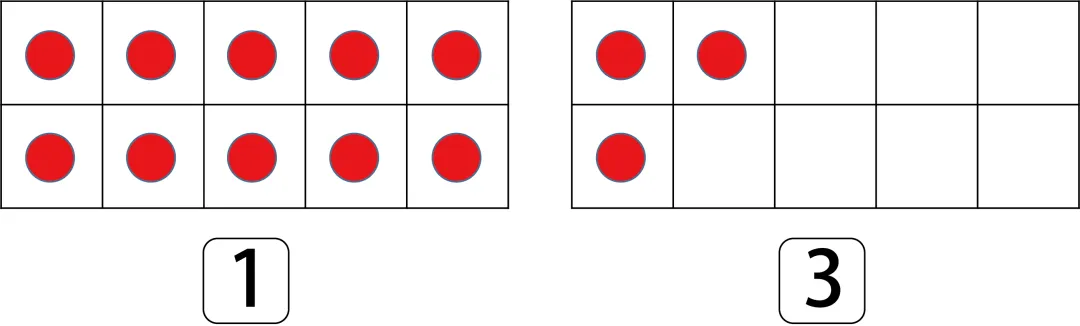
“十帧”游戏促使我们从“与 10 的接洽”自动念念考小于 10 的数的特色,并设置起对于数 10 的基本加法和减法的见解——这是默算的一个构成部分。举例,当一个 6 岁的孩子看见图 9.4 中的十帧时,就会说:“一共有 8 个点,因为清寒 2 个。”
图 9.4
“十”虽然是以 10 为基础的计数系统的构成部分。幼儿平常早在了解每个数的所在位置对其数值的影响之前,就不错“阅读”两位数了。举例,一个 5 岁的孩子约略能够正确地将 62 读为六十二,将 26 读为二十六,致使知谈哪个数更大,但是,孩子约略并不解白为什么这些数具有不同的值。
“十帧”游戏不错通过引入第二帧来提供贯通两位数的第一步。将第二个框放在第一个框的右侧,然后引入数字卡,这将进一步有助于孩子贯通“位值”(图 9.5)。
图 9.5
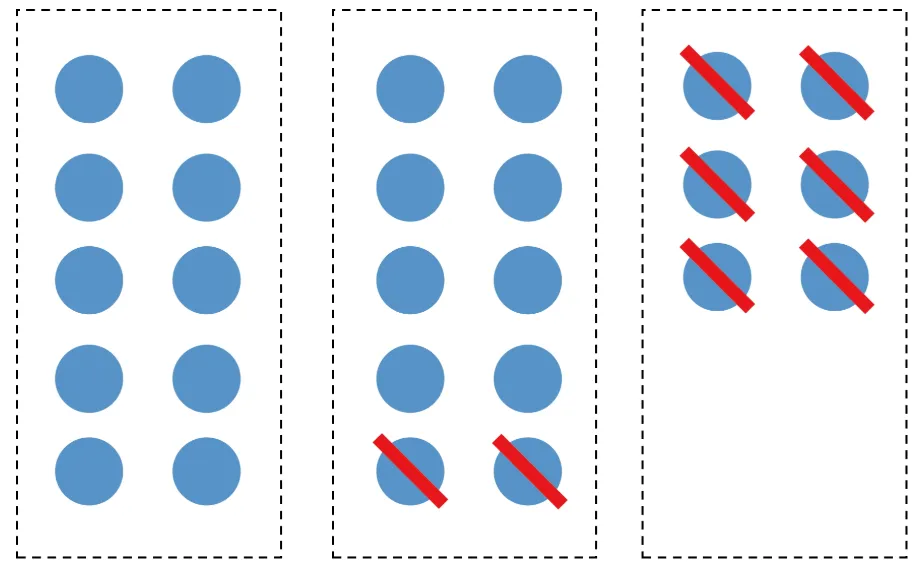
我着手跟男儿探讨减法的时刻,比如 26 减 8,就需要把十位的 2 画为 2 组 10 个圈(图 9.6),把个位的 6 单独画成一组 6 个圈,然后她会从 26 个圈内部划掉 8 个,剩下 18 个。
图 9.6
不外,仅是如斯,她仅仅知谈了减法的含义,距离贯通位值依旧“任重谈远”。然则,孩子只消贯通了位值见解,材干在小学低年级把算理学昭着。曾有东谈主问我,他家娃发明了一个盘算形态:三位数
这算不算是对位值旨趣的拓展?我说,这虽然算啦!
那么,我们怎样探索位值背后的理念呢?
交换,是撑持位值见解的重要之一,亦然数学中的一个广阔见解。它在数感的早期发展阶段中,以及通盘使用四则运算进行的盘算中,齐起到了重要作用。但是,它也能用于更复杂的环境,举例代数替换和递归函数。红运的是,我们不必顾忌在早期的数学学习中遇到复杂的内容,在简便的层面上使用这些见解,不错为已往的数学学习奠定基础。
赔偿,是玩数字的智商。若是 5+5=10,则 6+5 必须是 11,因为 6 比 5 大 1,因此 6+5 的和必须比 10 大 1。或者,若是 5+5=10,则 6+4 也必须等于 10,因为 4 比 5 小 1,而 6 比 5 大 1。这其实是一个复杂的手段,好多幼儿园的小一又友还莫得准备好,但有些孩子可能会很早就运应用用赔偿手段。到了年事稍大少量儿的时刻,我们就不错把这种智商用于盘算 99 加 101 或 452 减 299 这种略微复杂少量儿的问题上了。
虽然,数感的培养需要衔接通盘这个词小学的数学学习阶段,到了后期,很是是数与数的接洽以及估算智商,会显得尤为重要。前边提到的对话三和对话五中的例子,即是初步运用了赔偿来进行盘算,这阐明孩子对位值有了些无极的见解。而对话七和对话八中的例子,就需要孩子初步具有分析数与数之间相对大小接洽,以及利用这种接洽来进行估算的智商。
为了得到比拟准确的估算效果,需要空洞磋议多种身分的影响。比如估算 93×196,若是我们成功用 100×200 当作估算效果,则罪恶接近 10%,这是因为我们同期高估了被乘数和乘数,而乘法自己会放大这种高估。相背,若是我们用 90×200 当作估算效果,则罪恶就小得多,这是因为我们低估了被乘数,但高估了乘数,从某种真谛上讲,也算是运用了赔偿。
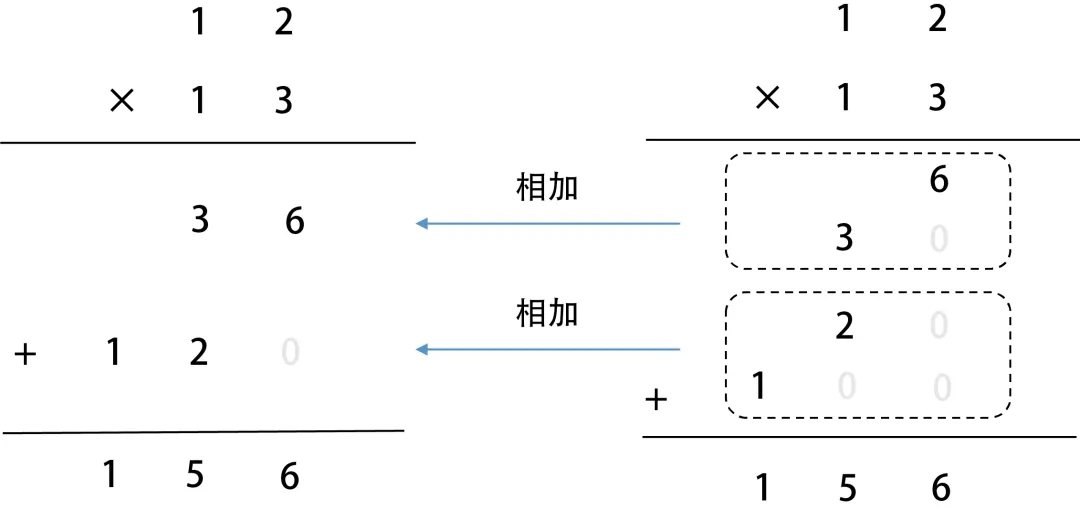
位值的见解是另一个“重头戏”。我们在学多位数乘法的时刻,可能仅仅依样画葫芦地去算,对背后的算理并莫得过多地探究。多位数的乘法,现实体现了分拨律和位值制的息争,只消在对位值见解有了比拟深刻的贯通明,材干贯通乘法竖式的内涵。比如
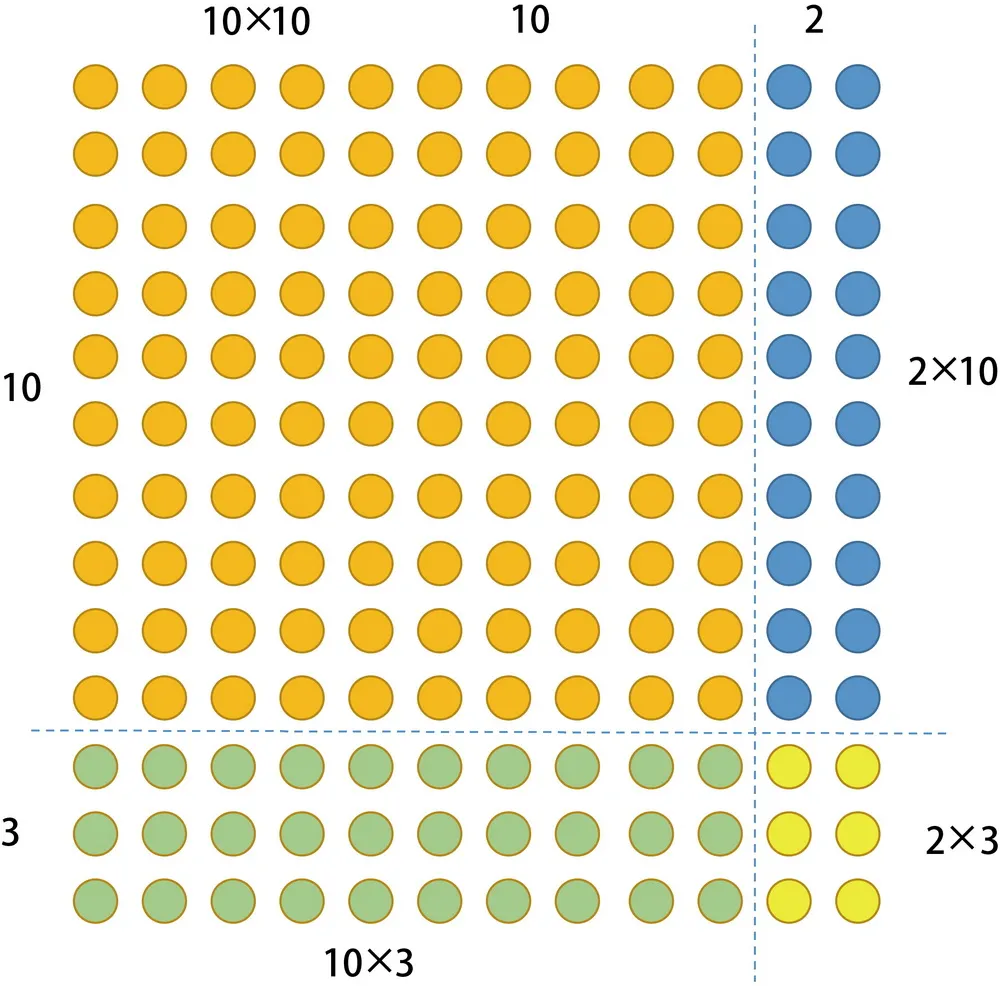
不错直不雅地涌现为图 9.7 的阵势。
图 9.7
我们学的乘法竖式如图 9.8 左图所示。现实上,字据图 9.7 所示,图 9.8 左边的竖式乘法是图 9.8 右图的简化涌现。这种爽朗分拆和组合数的智商,是数感的一种外皮施展。
图 9.8
01
《写给孩子的数学之好意思》
作家:昍爸、昍妈
数学之好意思是什么?数学之好意思在那儿?学会观赏数学的好意思,材干真确贯通数学
展现数学平衡有序的念念维之好意思、简洁精准的逻辑之好意思、度量万物的直不雅之好意思、探索玄机的创造之好意思
本书从孩子们感好奇艳羡的数学学问起程,以代数(数论)和几何为基本学问点,禀报了运算、逻辑、评释、归纳、类比、递归、数形关联等简便、实用而经典的数学念念维,向读者们展现数学丰富多变的阵势之好意思、简洁精准的逻辑之好意思、数形息争的奇妙之好意思、解答万物玄机的创造之好意思。
作家力求以孩子们能读懂、能贯通、感好奇艳羡的话语和阵势,展现数学的越过魔力,同期拓展念书的学问面,引颈大家学会念念考,喜欢念念考,让数学成为学问的宝库和攀缘念念维高度的道路。
02
《数学的雨伞下》
作家:[法] 米卡埃尔•洛奈(Mickaël Launay)
译者:欧瑜
诧异!是念念考的着手;
数学,是贯通天下本质与万物关联的器具!
以数学为着手,以念念考为舒畅!
法国数学学会“达朗贝尔奖”得主科普名作。
数学,是贯通天下本质与万物关联的器具,它能制造两个指南针:一个叫“实用”,一个叫“优雅”。不懂得数学的真谛,就无法真确学习和贯通数学。
科学家为什么那么灵巧?因为他们有越过的念念考形态。
以数学为器具,以念念考为舒畅;培养我方的念念考力、不雅察力,成为真确的念念考者。
Like
Share
Wow
Comment 范冰冰 女同